Filter by tag
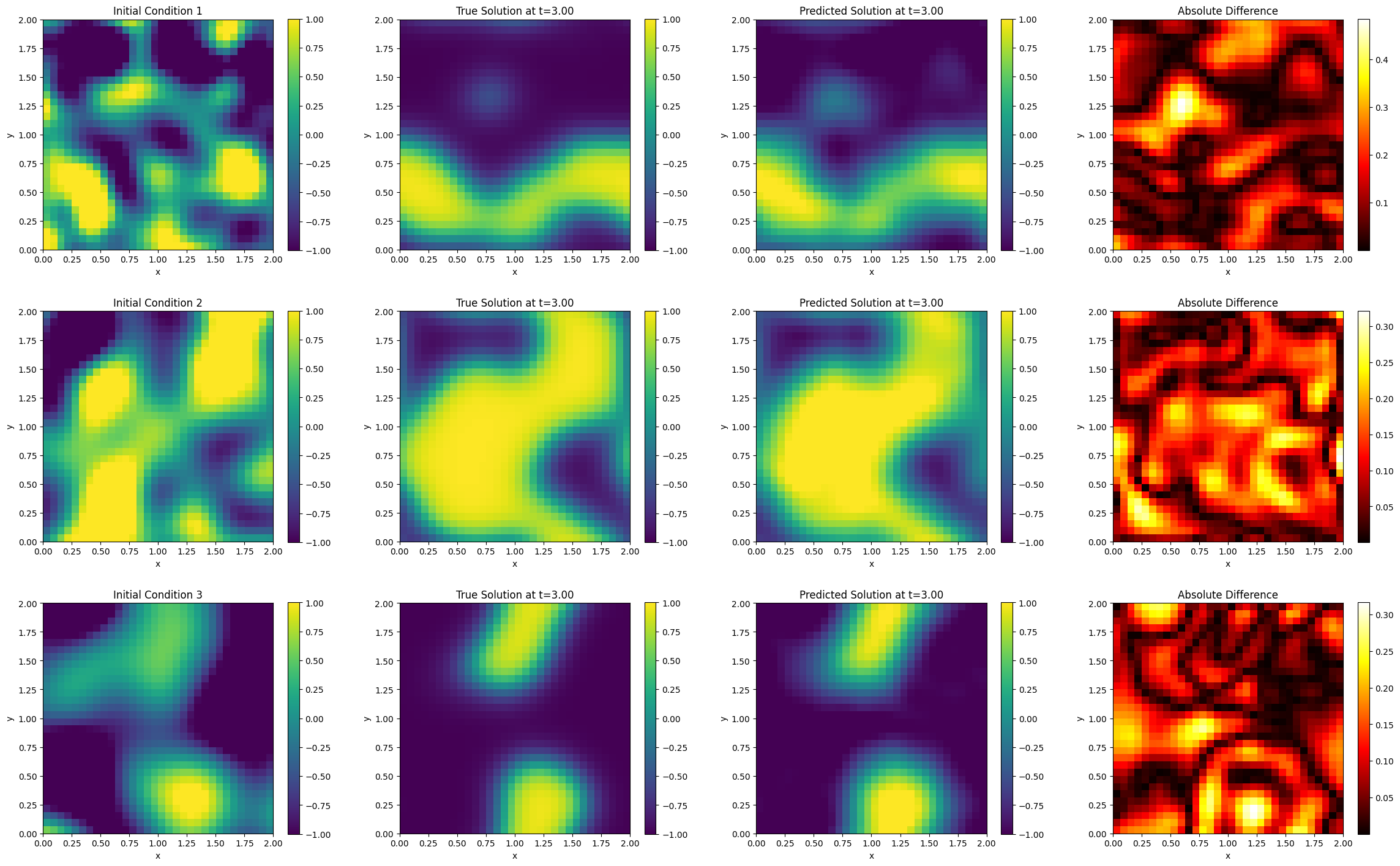
SciML: Allen-Cahn Equation via Modified DeepONet
Python project that implements a modified Deep Operator Network (DeepONet) to solve the Allen-Cahn equation. The project focuses on using neural networks to approximate the solution operator for this equation.
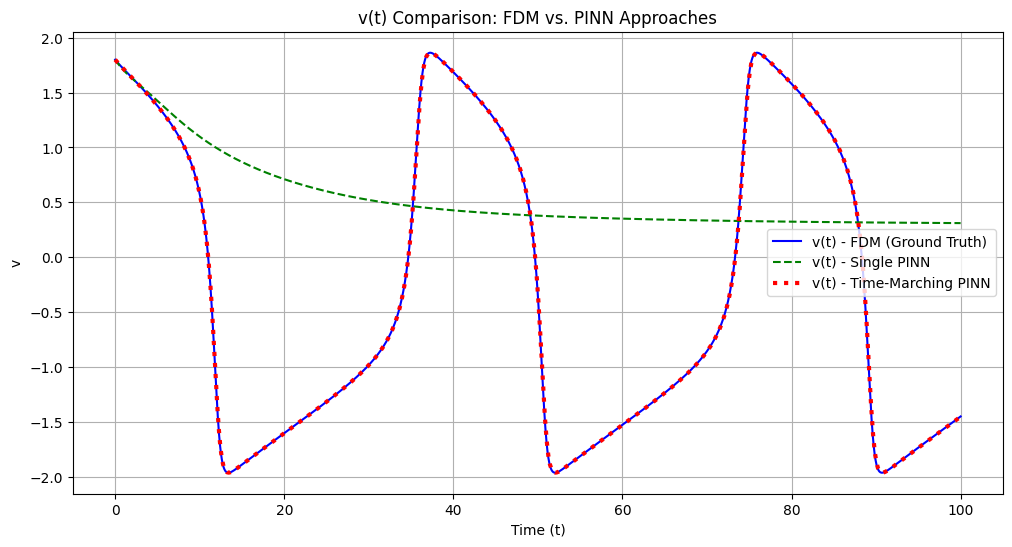
SciML: FitzHugh Nagumo Equation via Extended Physics Informed Neural Networks (XPINN)
Python project that utilizes Extended Physics Informed Neural Networks (XPINN) to learn the multiple time scale dynamics for the FitzHugh-Nagumo equation.
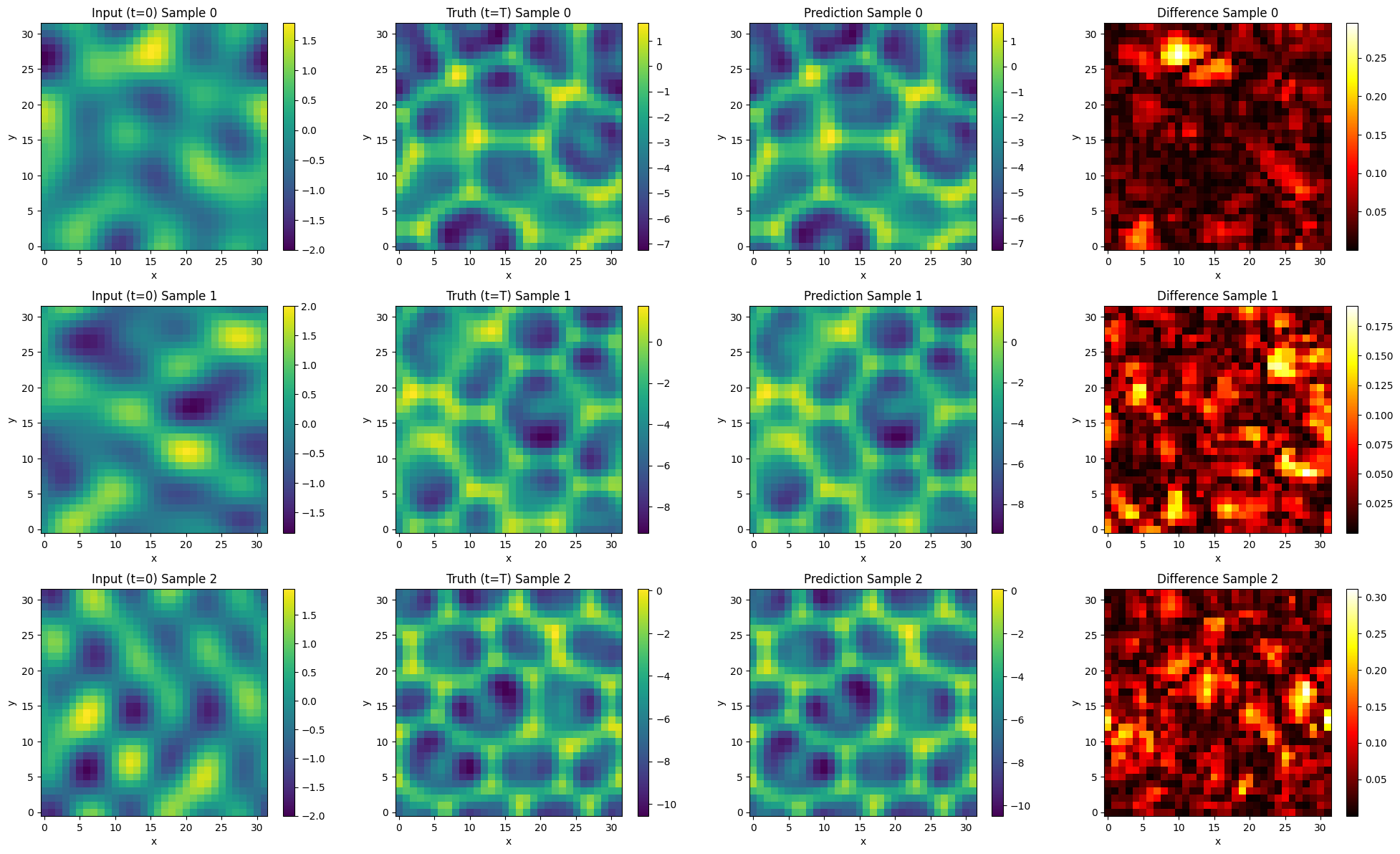
SciML: 2D Kuramoto-Sivashinsky Equation via Fourier Neural Networks (FNO)
Python project that employs Fourier Neural Networks to learn the solution operator for the 2D Kuramoto-Sivashinsky equation.
Dynamical Bestiary: Kuramoto-Sivashinsky Equation
Python notebook for the Kuramoto-Sivashinsky equation. Explores pattern formations using numerical continuation and direct simulation methods.
Dynamical Bestiary: Swift-Hohenberg Equation
Python notebook for the Swift-Hohenberg equation. Explores pattern formations using numerical continuation and direct simulation methods.
Dynamical Bestiary: Cahn-Hilliard Equation
Python notebook for the Cahn-Hilliard equation. Explores pattern formations using numerical continuation and direct simulation methods.
SciML: Burger's Equation via Physics Informed Neural Networks (PINN)
Python project that utilizes Physics Informed Neural Networks (PINN) to learn the solution operator for Burger's equation.
SciML: Damped Harmonic Oscillator via NeuralODE
Python project that employs Neural Ordinary Differential Equations (NeuralODE) to learn the dynamics of a damped harmonic oscillator.
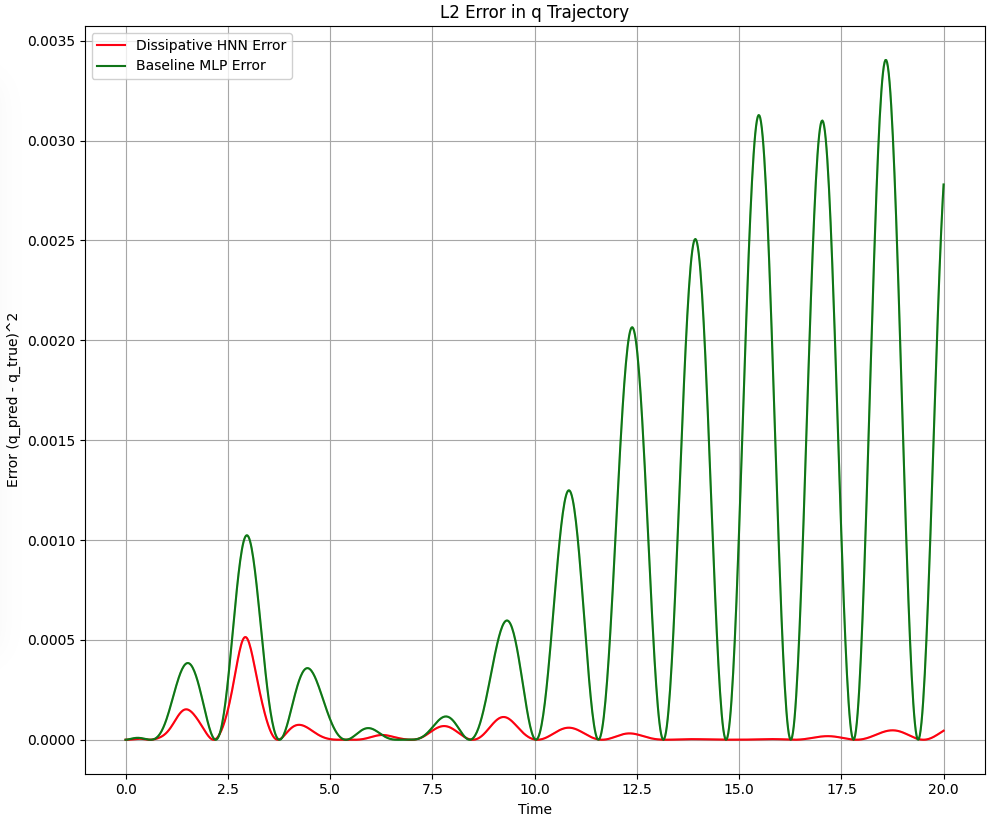
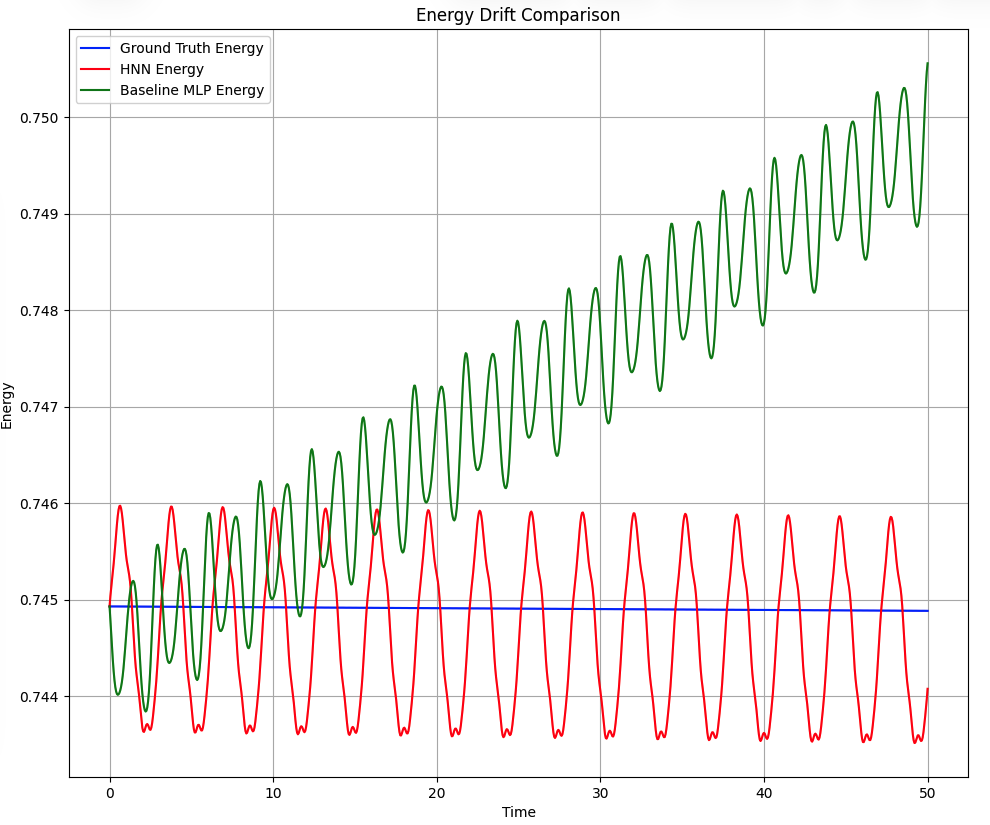
SciML: Damped Mass-Spring System via Hamiltonian Neural Networks (HNN)
Python project that utilizes Hamiltonian Neural Networks (HNN) to learn the dynamics of a mass-spring system, focusing on modeling the energy-dissipation properties of the system using neural networks.
SciML: Mass-Spring System via Hamiltonian Neural Networks (HNN)
Python project that utilizes Hamiltonian Neural Networks (HNN) to learn the dynamics of a damped mass-spring system, with a focus on modeling the energy-conserving properties of the system using neural networks.
SciML: 2D Darcy Flow and 1D Kuramoto-Sivashinsky via Fourier Neural Networks (FNO)
Minimal Python projects that employs Fourier Neural Networks to learn the solution operator for 2D Darcy Flow and the 1D Kuramoto-Sivashinsky equation.
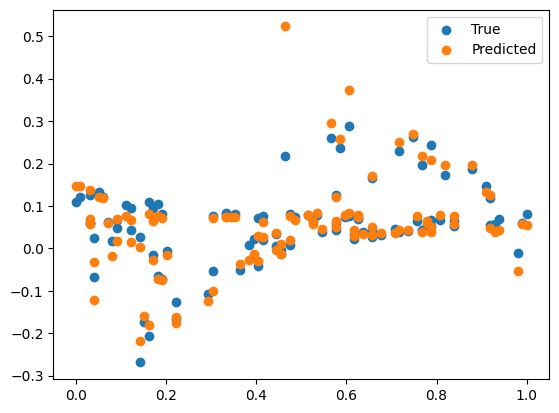
SciML: Advection Diffusion via DeepONet
Python project that uses Deep Operator Networks (DeepONet) to learn the solution operator for the advection-diffusion equation.
Dynamical Bestiary: Allen-Cahn Equation
Python notebook for the Allen-Cahn equation. Explores pattern formations using numerical continuation and direct simulation methods.
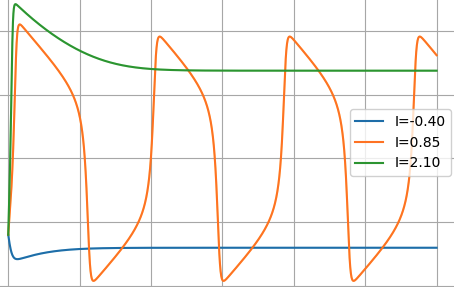
Dynamical Bestiary: FitzHugh-Nagumo Equation
Python notebook for the FitzHugh-Nagumo equation. Explores pattern formations using numerical continuation methods.
Dynamical Bestiary: 2D FitzHugh-Nagumo Equation with Spirals and Turing Patterns
Python notebook for the 2D FitzHugh-Nagumo equation. Explores spiral wave solutions and Turing patterns using finite difference methods.
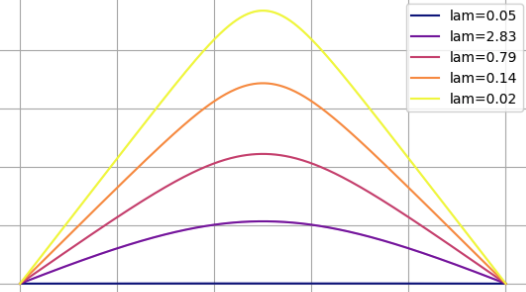
Dynamical Bestiary: Bratu Equation
Python notebook for the Bratu equation. Explores pattern formations using numerical continuation methods.
Spiral Waves in the Theta Model
MATLAB project that explores spiral wave solutions in the theta model through a PDE formulation using time stepping and numerical continuation methods.
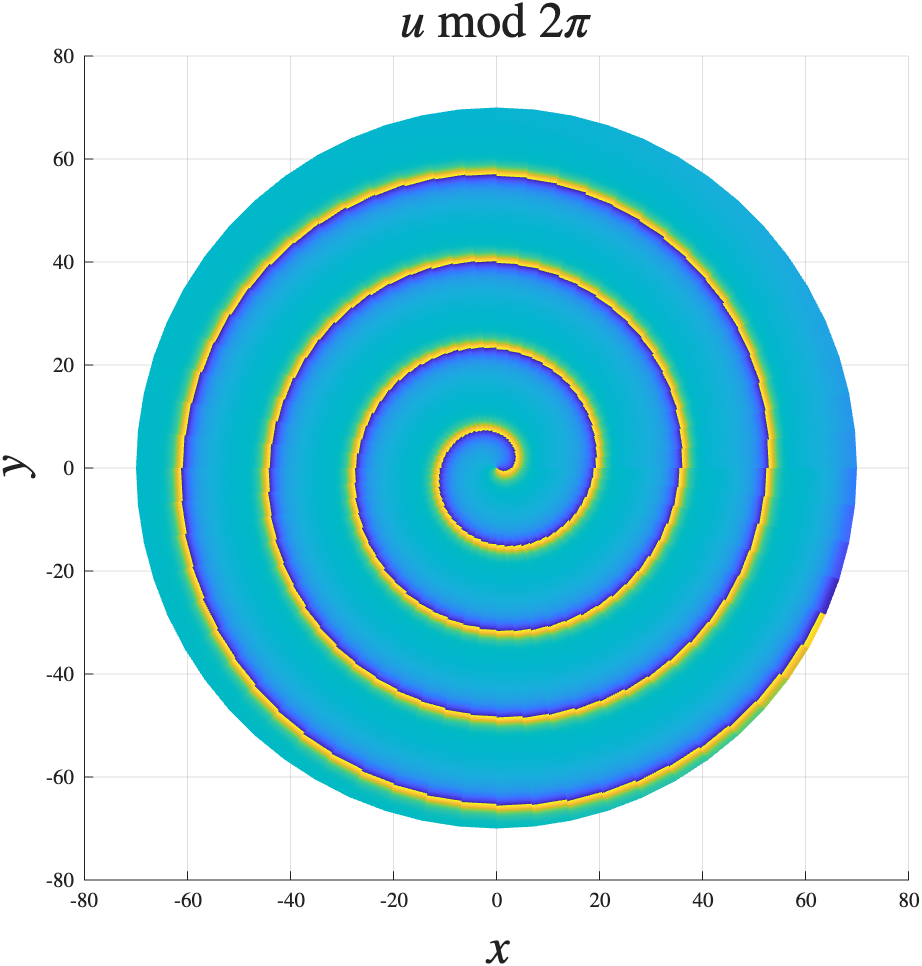
Spiral Waves via Geometric Flows
MATLAB project that simulates 2D spiral waves using geometric flows. The simulation visualizes the formation and evolution of spiral wave patterns in a two-dimensional space.